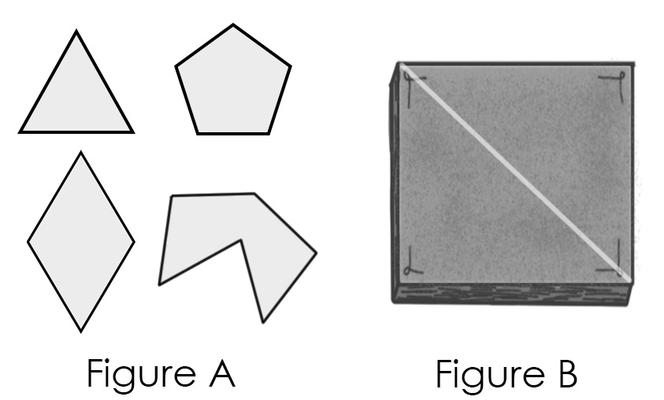
Chacun a ses petites manies : Sophus, lui, n’aime manger que des gâteaux équilatéraux. En géométrie, un polygone équilatéral est une figure dont tous les côtés sont rectilignes et de même longueur. Le plus connu est bien sûr le triangle équilatéral, mais on peut aussi trouver dans cette catégorie les losanges, certains pentagones et tout un tas de figures plus ou moins bizarres (Figure A).
Or voilà qu’un jour Sophus rentre de la pâtisserie avec un gâteau carré et l’égoïste intention de le manger tout seul, lorsqu’il trouve devant sa porte son ami Ludwig, qui vient lui rendre visite. A moitié à contrecœur, il lui propose de partager.
Ils ouvrent la boîte et Ludwig suggère de couper le gâteau en deux par la diagonale pour faire deux beaux triangles identiques (Figure B). Car c’est là sa manie : tout gâteau doit être partagé en parts de formes et de tailles rigoureusement identiques. Mais Sophus l’arrête. Hors de question : la diagonale du carré est plus grande que ses côtés, ce triangle n’est pas équilatéral !
Pour satisfaire à la fois Sophus et Ludwig, est-il possible de couper ce gâteau carré en deux parts équilatérales identiques ? Et, si oui, combien de côtés ce polygone pâtissier devra-t-il avoir au minimum ?
Il vous reste 3.84% de cet article à lire. La suite est réservée aux abonnés.




